神经元的建模

Hodgkin-Huxley 模型

HH 模型是最经典的生物真实度最高的单神经元动力学模型。由 Hodgkin 和 Huxley 在 1952 年基于乌贼巨轴突的实验建立。它详细描述了神经元膜上的离子通道动力学，适用于精确研究神经元的生物电学特性。

以下方程在理论上描述了神经元的发放活动：

$$ C_m\frac{dV}{dt}=-g_{Na}m^3h(V-E_{Na})-g_{k}n^4(V-E_k)-g_l(V-E_L)+I $$

其中：$C_m$是膜电容，$g_i$为对应通道开放时的最大电导（$Na,K$代表对应离子的门控离子通道，$L$代表漏电流离子（通常是K离子）通道），m、n则代表这量种离子通道一个亚基开放的几率，而h则表示钠离子通道失活阀门打开（即通道打开）的概率；它们的大小由膜电位决定，并存在一定函数关系：

$$ \frac{di}{dt}=\alpha_i(1-i)-\beta_ii $$

$\alpha_i,\beta_i$分别为对应对应亚基由关闭转为开放和由开放转为关闭的概率

而$\alpha_i$与$\beta_i$经实验测得到以下和膜电位相关的函数关系：

$$ \begin{cases} \alpha_n=\frac{0.01\times(-50-U)}{e^{\frac{-50-U}{10}}-1} \qquad\beta_n=0.125\times e^{\frac{-60-U}{80}}\\ \alpha_m=\frac{0.1\times(-35-U)}{e^{\frac{-35-U}{10}}-1} \qquad\beta_n=4\times e^{\frac{-60-U}{18}}\\ \alpha_h=0.07\times e^{\frac{-60-U}{20}}\qquad\beta_n=\frac{1}{e^{\frac{-30-U}{10}}+1} \end{cases} $$

该模型理论上能在很高的精度上对单个神经元的发放进行模拟，但由于引入的参数较多计算复杂度极高，在实际运用中大量的浮点数计算（120次每个神经元）使得该模型并不适合对大量神经元组成的网络进行模拟；而只能在神经元数量较少的系统中使用。

Leaky-integrate-fire model

LIF 模型是最简单的神经计算模型，它近似描述了神经元的输入-输出行为，而不考虑离子通道细节。LIF 适用于计算神经科学，尤其是大规模神经网络模拟。

该模型的核心方程如下：

$$ \begin{cases}C_m\frac{dV}{dt}=-g_l(V-E_L)+I\qquad\qquad\quad\\ if\quad V\ge V_{threshold}\quad then\quad V\rightarrow V_{reset}\end{cases} \tag1 $$

即：如果 V 没有达到 $V_{threshold}$​，它只是被动地泄漏并整合输入电流 $I$。如果 V 达到 了$V_{threshold}$​，神经元“发放”一个脉冲，并立即重置为$V_{reset}$​。

其中上述方程中符号含义与HH模型中的相同。

LIF模型作为极为简化的模型常用于大规模神经网络的模拟，比如SNN（脉冲神经网络）。除此之外，由于其模型极度简化，研究者可以任意对模型的任何部分进行个性化的“完善”从而满足使用者的需求。当然若是从各个方面都对其进行完善这个模型终将会变回HH模型的样子。

对于LIF来说，其优点也是其缺点，由于极度的简化，他已经失去了大部分生理学信息，不在能够反映神经元发放的各种细节与特性。

Izhikevich 模型

Izhikevich 模型是 LIF 模型和 HH 模型的折中，它能模拟复杂的神经元放电模式，同时保持较低计算成本。适用于大规模神经网络，同时能模拟现实神经元的适应性放电、簇状放电等复杂行为。其核心方程为

$$ \begin{cases}\frac{dV}{dt}=0.04V^2+5V+140-u+I\\ \frac{du}{dt}=a(bV-u)\\ if \quad V\rightarrow c \quad then\quad u\rightarrow u+d \end{cases} $$

其中：V为膜电位，u为恢复变量（由钾和钠的回复电流影响），I为包含突出电流和人工输入的刺激电流，而a,b,c,d则表示调控神经元放电模式的参数（a与电位回复的时间有关，b与静息电位的波动范围有关，c与动作电位发放后的Vreset有关，d描述了由缓慢的高阈值Na+和K+电导引起的恢复变量u的尖峰后复位。）

值得注意的是，方程中的$0.04V^2+5V+140$项是作者对神经动作电位发放做了大量拟合得来的。

如右图（Izhikevich，2003）所示，可以看出该模型能够基本复现小鼠运动皮层的几类神经元的发放模式，但仍有细节上有失偏颇（如：Ureset与Urest之间的差距；f在时域上的变化等）但总体上能够模拟出神经元的基本模式。

总结

对于神经元的动力学模型来说最重要的是能够模拟其发放特征，在Izhikevich2004年的论文中明确指出了20种神经元的发放行为，并对数个模型进行了评估。其评估结果如下：

1. H-H模型作为生物真实度最高的单神经元动力学模型拥有极高的运算复杂度且能在理论上模拟神经元的所有发放行为。

2. LIF模型作为另一个极端，拥有极低的运算复杂度但是仅能复现出三种神经元发放行为。

3. 而作者本人的模型则融合了两者的优点，在低运算复杂度的同时能够模拟出所有种类的神经元发放模式，其唯一的不足就是生物真实性较差。

突触的建模

生理学模型

突触后离子通道电流: $$ -I_{syn}=-g_{syn}(U-E_{syn}) $$ 其中g为电导, E为反转电位. 进一步的,我们定义: $$ g=\bar{g}f\quad \bar{g}=g_{max} , f=f(D,t) $$ f代表离子通道打开的比率, 是突触间隙神经递质浓度D和𝑡的函数. 进一步,我们假定离子通道的打开比率f依赖如下动态转化关系:

1. 关闭的通道转变为打开的比率α，依赖神经递质浓度
2. 打开的通道转变为关闭的比率β，不依赖递质浓度 因此有以下ODE表征f: $$ \frac{df}{dt}=\alpha(1-f)-\beta f $$ 当突触间隙内的神经递质浓度变化速度很快时,我们可以有以下近似: $$ \frac{df}{dt}=\alpha’\delta(t-t_0)(1-f)-\beta f $$ 其中$t_0$为神经递质释放的时刻, α’ 为常数项(与神经递质浓度无关).

对于结构较为特殊的离子通道如: NMDA离子通道, 其孔道中有一个常态$Mg^{2+}$阻碍物质的通过,因此 $$ -I_{syn}=-g_{syn}(U-E_{syn})\quad 变为:\quad -I_{syn}=-g_{syn}b(U,[Mg^{2+}])(U-E_{syn}) $$

经测算: $b=\left(1+e^{-0.062U}\frac{[Mg^{2+}]}{3.57}\right)^{-1}$

现象学模型

省去生理学模型中突触后电压对突触的影响后,得到: $$ -I_{syn}=-g_{syn} $$ 设电导的上升和衰减满足以下ODE:

$$ \frac{df_{rise}}{dt}=-\frac{f_{rise}}{\tau_{rise}}\quad \frac{df_{decay}}{dt}=-\frac{f_{decay}}{\tau_{decay}} \tag2 $$

那么电导的变化过程相当于:

$$ g(t)\propto f_{decacy}(t)-f_{rise}(t) $$

求解(2)中常微分方程得:

$$ f_{rise}(t)=e^{-\frac{t-t_0}{\tau_{rise}}}\quad f_{decay}(t)=e^{-\frac{t-t_0}{\tau_{decay}}} $$

代入公式得:

$$ \begin{gathered} g(t)=g_{max}\left(e^{-\frac{t-t_0}{\tau_{decay}}}-e^{-\frac{t-t_0}{\tau_{rise}}}\right)H(t-t_0)\\ 亦写作: \quad g(t)=\sum_kg_{max}e^{-\frac{t-t_k}{\tau}}\left(1-e^{-\frac{t-t_k}{\tau_{rise}}}\right)H(t-t_k)\\ \end{gathered} $$

其中H为阶跃函数,$\tau_{decay}(\tau)$为衰减常数, $\tau_{rise}$为上升常数,k为发放标号. 在HH模型中, 突触电流可以作为突触后神经元的输入,如:

$$ C_m\frac{dV}{dt}=-g_{Na}m^3h(V-E_{Na})-g_{k}n^4(V-E_k)-g_l(V-E_L)+I\qquad I=I_{syn} $$

突触可塑性

STDP——Spike-Timing-Dependent Plasticity

• STDP是一种神经可塑性机制，描述了神经元突触的强度如何根据突触前后两个神经元的活动时间顺序而改变.
  • 当突触前神经元在突触后神经元之前放电时，通常会导致突触强度增强
  • 当突触前神经元在突触后神经元之后放电时，通常会导致突触强度减弱 突触强度的调节有助于大脑学习和记忆等神经功能的实现.

STDP 利用了一种非监督的赫布学习方式, 其学习方式是依据两个神经元的放电顺序来改变两个神经元之间连接的权重$\Delta w$: $$ \Delta w\begin{cases} A_{+}e^{\frac{t_j^{pre}-t_i^{post}}{\tau_{+}}}, \qquad if\quad t_j^{pre}\le t_i^{post}\\ -A_{-}e^{-\frac{t_j^{pre}-t_i^{post}}{\tau_{-}}}, \qquad if\quad t_j^{pre}\gt t_i^{post} \end{cases} $$ 其中$A_+$是突触增强学习率; $A_-$是突触减弱学习率; $\tau_+$是增强指数衰减时间常数; $\tau_-$ 是减弱指数衰减时间常数.

SNN——脉冲神经网络（Spiking neuron models）

一个神经元网络应该由神经元组成, 网络的性质取决于:

1. 神经元模型的类型
2. 突触模型的类型
3. 突触学习的规则
4. 输入的编码、输出的解码

不同于ANN和DNN, 虽然他们都是启发自脑, 但SNN却保留了脑的基本结构单元(神经元和突触)并采用了类似生理学大脑的连接. 并且在硬件上,SNN也常采用具有神经形态学的大规模集成电路而非常规的集成电路

兴奋抑制平衡网络

实际上, 生物脑的放电具有高度不规则, 低相关性, 电压处于阈值附近的特征, 这与一直以来建立的传统的稳定模型不符, 因此(Van Vreeswijk & Sompolinsky, 1996) 提出是否可以在兴奋-抑制强耦合、强噪声的网络里,自发的产生无序、类混沌的放电模式, 同时保持网络活动稳定?

他们构建了一个大规模随机连接的SNN, 包含$N_E$个兴奋性神经元和$N_I$个抑制神经元. 单个神经元的放电率呈泊松型/指数分布. 神经元之间以概率P相互连接, 从而每个神经元接收大量的兴奋和抑制输入并且他们相互抵消使整个网络整体维持在亚阈值状态.(有效避免网络过度兴奋或过度抑制)

尽管兴奋和抑制的输入平衡,但是瞬时的波动可以很大, 这些波动驱动神经元无规则且无序的放电. 与此同时, 即使是很小的波动也会导致后续放电轨迹发生较大的变化, 使得整个网络处于不存在稳定固定点(周期轨道)的混沌态.

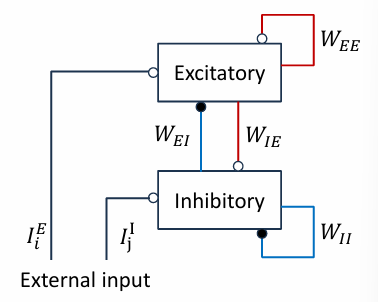
网络动力学模型推导

假设: 为保证稀疏连接,要求:$1\ll K\ll N$,即P较小. 由(1)(或者H-H模型,这里简单起见只考虑LIF)可知膜电位方程满足以下形式: $$ C\frac{dU}{dt}=-gU+I_{input} $$ 进一步的有: $$ \begin{gathered} CR\frac{dU}{dt}=-RgU+RI_{input}\\ \tau\frac{dU}{dt}=-U+RI_{input} \end{gathered} $$ 这里$\tau$被称为膜时间常数,表征膜电位对输入信号相应的快慢.

连续神经元模型 把神经元建模成一个连续变量（如膜电位、电流或放电率）随时间变化的微分方程，而不是像脉冲神经元模型那样只记录离散放电事件。 经典形式: rate model——$r(t)=f(u(t))$, 其中f(u)是放电率-膜电位关系的激活函数（例如 sigmoid 或 ReLU）

若用$r_j^E$表征第j个兴奋神经元的脉冲率, 那么在激活函数的映射下:$f(r_j)$则表征第j个神经元产生的电流,此时可以计算出网络的兴奋输入总和:

$$ \tau\frac{dU_i^E}{dt}=-u_i^E+\sum_{j=1}^{K_E}W_{EE}f(r_j^E)-\sum_{j=1}^{K_I}W_{EI}f(r_j^I)+I_i^E $$

其中等号右边第二项为:其他EN对第i个EN的input, 第三项为: IN对第i个EN的input; $u_i$和$I_i$分别为漏电流和外界输入,W为权重,K为与目标神经元有连接的神经元数目.

同理,网络的抑制输入总和:

$$ \tau\frac{dU^I_i}{dt}=-u_i^I+\sum_{j=1}^{K_E}W_{IE}f(r_j^E)-\sum_{j=1}^{K_I}W_{II}f(r_j^I)+I_i^I $$

要满足网络的上述条件, 要求达到输入电流均值平衡, 进一步的, 还有方差平衡, 在平均场理论下即:

$$ \begin{gathered} \sum_{j=1}^{K_E}W_{EE}f(r_j^E)+I_{i}^{E}\approx\sum_{j=1}^{K_I}W_{EI}f(r_j^I)\\ Var(I_i^E(t))=Var(\sum_{j=1}^{K_E}W_{EE}f(r_j^E))+Var(\sum_{j=1}^{K_I}W_{EI}f(r_j^I)) \end{gathered} $$

进一步:

$$ \begin{gathered} K_EW_{EE}-K_IW_{EI}\sim O(1)\\ K_E(W_{EE})^2+K_I(W_{EI})^2\sim O(1) \end{gathered} $$

兴奋-抑制平衡网络的意义

1. 网络动态范围线性化: 在网络平衡的工作状态下，兴奋性和抑制性神经元的发放率随外界输入电流强度的增加而线性增加
2. 对外界刺激的快速响应: EI平衡网络处于临界态，以便能快速对外部刺激做出响应
3. 信息保真度高,信息容量大,动态范围?

决策神经网络

Xiao-Jing Wang 在2002年的工作中(Wong & Wang, 2006)中指出, 决策 = 兴奋-抑制平衡网络中竞争性证据积累 + 噪声扰动 + 阈值判定,即不同的选项由不同的神经元群代表, 选项之间的竞争表征为神经元群之间的竞争, 代表不同选项的神经元群相互抑制形成竞争,哪一组神经元群取得优势,代表着对应的选项被选择.

Xiaojing Wang老师2002年论文中使用的决策神经网络是由如图所示：一个抑制神经元群和两个与之相连且彼此独立的兴奋神经元群组成。两个兴奋神经元群通过抑制神经元群影响对方的兴奋程度，一旦其中一个神经元群占有优势，它内部的兴奋信号将快速变强并通过抑制神经元群将对方的活动抑制到最低点，形成winner take all(赢者通吃)的局面。

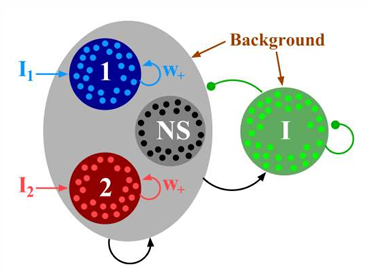
动力学方程 由LIF模型可知，神经元j的膜电位满足以下方程：

$$v_j^{(i+1)}=v_j^{(i)}+\frac{dt}{\tau_m}\left[-(v_j^{(i)}-v_{rest})+I_{synapse,j}^{(i)}+I_{input,j}^{(i)}\right]$$

其中：

$$ I_{synapse,j}^{(i)}=I_{ampa,j}^{(i)}+I_{nmda,j}^{(i)}+I_{gaba,j}^{(i)} $$

对于输入的外部电流，在模型中符合泊松输入， 而对于突触电流，由突触电流模型可知：

$$ I=g\cdot(E-v)\qquad \text{其中E为对应受体门控通道的反转电位，g为对应电导} $$

特别的，对于NMDA受体门控通道，因为其通道内部含有$Mg^{2+}$阻断机制其电流公式需要稍加修正：

$$ I_{NMDA}=\frac{g_{NMDA}\cdot(E_{NMDA}-v)}{B(v)}\qquad \text{其中阻断因子：}B(v)=1+\frac{[Mg^{2+}}{3.57}\cdot e^{-0.062v} $$

上式中，各受体门控通道的电导由权重和突触变量的线性组合决定：

$$ g_{\alpha,j}=\sum_k\omega_{\alpha,j,k}\cdot s_{\alpha,k}\qquad \text{其中α代表受体门控通道类型；k代表与第j各神经元相连接的其他神经元} $$

突触变量是表征突触活动状态的动态参数，在触发神经元放电时s瞬间增加随后随着时间按照如下方程衰减：

$$ \frac{ds_{syn}}{dt}=-\frac{s_{syn}}{\tau_{syn}}+\sum_k\delta(t-t_k^{(j)})\qquad \text{即：}s_{syn}^{(i+1)}=s_{syn}^{(i)}\cdot\left(1-\frac{dt}{\tau_{syn}}\right)+\text{发放事件输入} $$

在神经元发放后，神经元进入不应期，膜电位将被重置：

$$ \text{If   } t-t_{lastspike}\lt\tau_{ref}\Longrightarrow v_j=v_{reset} $$

模型特点

1. 兴奋-抑制平衡: 维持网络处于临界动力学区间，易受小证据输入驱动
2. 证据积累特性: 网络可持续性记忆短期输入, 微弱偏好输入可以逐渐累积
3. 噪声主导的概率性决策: 随机噪声在平衡临界状态下放大使得决策结果存在概率性, 可以拟合心理物理学中的选择概率和反应时分布
4. 慢动力学: 兴奋性群体存在持续反馈且网络动态能停留在亚稳态，允许证据在秒级时间尺度内累积, 直至证据累积到达阈值

脉冲神经网络训练的困难

1. 梯度计算困难:
   • 脉冲神经网络非连续性和离散性使得无法直接应用梯度下降算法
   • 可以设计特殊的梯度估计方法，但效果不理想
2. 收敛缓慢:
   • 由于突触权重变化的离散性和非线性，造成脉冲神经网络的训练过程需要大量迭代才能收敛，效率较低
3. 参数敏感性:
   • 脉冲神经网络对一些超参数，如学习率、时间常数等非常敏感
   • 需要仔细调参，才能得到好的训练效果
4. 生物学可解释性不足:
   • 仍然缺乏对脑学习机制的解释性，需要进一步研究生物学上更贴近的学习规则
5. 应用范围有限:
   • 目前主要应用于感知类任务，在复杂的认知类任务上效果不佳

Bibliography

Izhikevich, E. M. (2003). Simple model of spiking neurons. IEEE Transactions on Neural Networks, 14(6), 1569–1572. https://doi.org/10.1109/TNN.2003.820440

Izhikevich, E. M. (2004). Which Model to Use for Cortical Spiking Neurons? IEEE Transactions on Neural Networks, 15(5), 1063–1070. https://doi.org/10.1109/TNN.2004.832719

[GitHub - juseong-kim/HH-Model: Hodgkin-Huxley MATLAB Model](GitHub - juseong-kim/HH-Model: Hodgkin-Huxley MATLAB Model)

Van Vreeswijk, C., & Sompolinsky, H. (1996). Chaos in Neuronal Networks with Balanced Excitatory and Inhibitory Activity. Science, 274(5293), 1724–1726. https://doi.org/10.1126/science.274.5293.1724