Hopfield 吸引子网络
吸引子网络有多种常见类型, 其中最简单的是hopfield网络模型.
网络结构
该网络由许多具有二值状态的神经元组成, 网络中每两个神经元之间都存在等权重的相互连接.
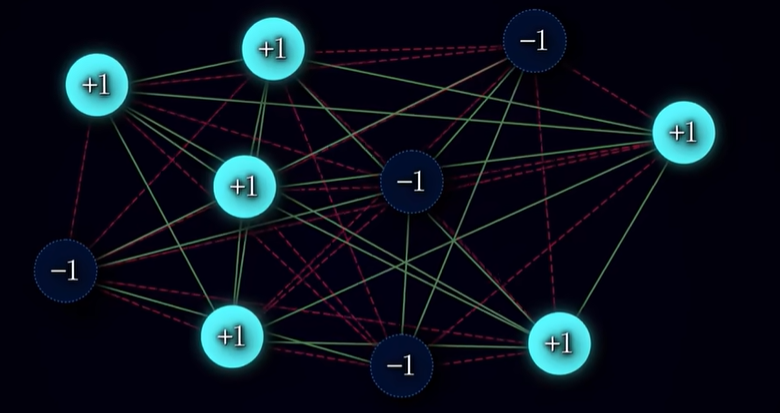
网络基本结构如上图所示, 各个神经元之间的没有顺序, 其连接也是饱和的 ,接下来介绍该网络的参数: N: 神经元数量 $s_i$: 神经元状态, 通常是二值的, 比如$s_i\in {-1,1}$ 分别表示神经元是否激活. $\boldsymbol{\xi}^\mu_i$: 第μ个模式(图像)中第i个神经元的状态$\mu \in {0, 1, …, P}$,P 为总的记忆模式(图像)数. $\omega_{ij}$:第i个神经元与第j个神经元之间的连接权重
网络运行模式
学习:
- 网络通过Hebb法则来学习改变神经元之间的连接权重1, 神经元之间的权重学习方式为:
$$ \omega_{ij}=\frac{1}{N}\sum^P_{\mu=1}\boldsymbol{\xi}^{\mu}_i\boldsymbol{\xi}^{\mu}_j\qquad i\ne j $$
- 其中$\omega$可正可负, 正值代表兴奋性突触, 负值代表抑制性突触.
- 初始向网络输入一组图样2$\vec{\chi}=[\vec{x_a},\vec{x_b},\dots]$ 每一个$\vec{x}$代表一个图样是一个N维向量, 向量的每一项都是$\pm1$,表征神经元的两个状态.
- 网络中的起始权重矩阵是一个全零矩阵; 图样输入到网络中后, 求出图样向量的外积(即求出对应大小的矩阵)随后加在全零矩阵上再对矩阵除以N以防止权重过大, 随后将矩阵中的自连项(i=j)化为0以除去自连 最终得到一个对角矩阵(因为wij=wji)
回忆:
- 输入图样: 向网络输入一个初始图样$\vec{s}=[+1,-1,\dots]$,网络会初始化所有神经元状态为 $\vec{s}$ 即图样矢量中的每一项都对应一个神经元的状态,.
- 随后逐个随机选择一个神经元更新它的 $s_i$ 的状态:
$$ s_i^{new}=sign(\sum_j\omega_{ij}s_j)\qquad 其中:\quad sign(X)=\begin{cases} X\lt 0 \longrightarrow -1\\ X\gt0\longrightarrow +1\\ X=0\longrightarrow0\end{cases} $$
- 上述步骤最终会因为神经元的状态不再改变而停下, 而这个稳定的状态就是一个吸引子, 代表着输入图样最接近的状态.
核心原理
最低能量原则
Hopfield网络定义了能量函数(Lyapunov function):
$$ E=-\frac{1}{2}\sum_{i,j}\omega_{ij}s_is_j $$
且在理论上输入学习对应的状态应在学习后对应能量极小的状态. 将连接权重公式代入上式得:
$$ \begin{gathered} E=-\frac{1}{2}\sum_{i,j}(\frac{1}{N}\sum_{\mu=1}^P\xi_i^{\mu}\xi_j^{\mu})s_is_j\\ =-\frac{1}{2N}\sum_{i,j}(\sum_{\mu=1}^P\xi_i^{\mu}\xi_j^{\mu})s_is_j\\ =-\frac{1}{2N}\sum_{i,j}\sum_{\mu=1}^P\xi_i^{\mu}\xi_j^{\mu}s_is_j \end{gathered} $$
令$s_i,s_j=\xi_i^{\nu},\xi_j^{\nu}$ ,则:
$$ \begin{gathered} E=-\frac{1}{2N}\sum_{i,j}\sum_{\mu=1}^{P}\xi_i^{\mu}\xi_j^{\mu}\xi_{i}^{\nu}\xi_j^{\nu} \\ =-\frac{1}{2N}\sum_{i,j}\left[(\xi_i^{\nu}\xi_{j}^{\nu})^2+\sum_{\mu \neq \nu}\xi_i^{\mu}\xi_j^{\mu}\xi_i^{\nu}\xi_j^{\nu}\right] \\ =\sum_{i,j}(1+\sum_{\mu\ne\nu}\xi_i^{\mu}\xi_j^{\mu}\xi_i^{\nu}\xi_j^{\nu})\\ =-\frac{N(N-1)}{2N}-\frac{1}{2N}\sum_{i,j}\sum_{\nu\ne\mu}\xi_i^{\mu}\xi_j^{\mu}\xi_i^{\nu}\xi_j^{\nu} \end{gathered} $$
由$\sum_{i\ne j}A_iB_j=\sum_iA_i\sum_jB_j-\sum_iA_iB_i$
$$ \begin{gathered} E=-\frac{N(N-1)}{2N}-\frac{1}{2N}\sum_{\mu\ne\nu}{[\sum_i(\xi_i^\mu\xi_i^{\nu})]^2-N}\\ E=-\frac{N(N-1)}{2N}-\frac{1}{2N}\sum_{\mu\ne\nu}[(\vec{\xi_i^\mu}\cdot\vec{\xi_i^{\nu}})^2-N] \end{gathered} $$
若$\vec{\xi_i^\mu}$与$\vec{\xi_i^{\nu}}$正交, 则:
$$ E=\frac{P-N}{2} $$
若将$\nu\ne\nu$的一项称为交叉项, 另一项称为主项, 那么由上述推导可以看出主项提供了能量E的主要负项,主项越大那么E越低. 特别的, 在$\vec{\xi_i^\mu}$与$\vec{\xi_i^{\nu}}$正交时,主项提供所有的负项, 因此当$s_i,s_j=\xi_i^{\nu},\xi_j^{\nu}$ 时(即输入为学习时的状态时)主项最大, 能量最低.
主项在能量景观中“挖出”深谷,对应记忆模式的稳定吸引子; 交叉项在能量景观中引入“噪声山丘”,可能掩盖或扭曲原有的深谷。

异步更新
根据异步更新公式:3 $$ s_i^{new}=sign(\sum_j\omega_{ij}s_j)\qquad 其中:\quad sign(X)=\begin{cases} X\lt 0 \longrightarrow -1\\ X\gt0\longrightarrow +1\\ X=0\longrightarrow0\end{cases} $$ 我们可以看出sign函数中的自变量$X=\sum_j\omega_{ij}s_j$乘上$s_i$就能够表征能量,也就是说根据X值得正负来调整$s_i$可以使得$s_iX$为正,从而E为负达到降低能量的目的. 因此sign(X)能够实现能量永远不高于上一步,使得网络能量逐步降低达到局部极小值.
正交性与容量限制
经典 Hopfield 网络能可靠存储的图样数量 $P_{max}$ 和神经元数 N 的关系是:$P_{max}\approx 0.138N$, 若超过这个数值就容易发生极易混淆(混合模式),错误召回,虚假稳定态等情况. 然而0.138来源自统计物理得大概估值, 在某些情况下并不适用——比如所有的$\vec{\xi_i^\mu}$与$\vec{\xi_i^{\nu}}$正交.
$\vec{\xi^\mu}$可以看作是高维空间中得向量, $\vec{\xi_i^\mu}$与$\vec{\xi_i^{\nu}}$正交意味着学习时输入的状态之间得干扰最小化,能量由主项主导,此时能量为:$E=\frac{P-N}{2}$.
- 当P<N时: 能量E<0, 网络能稳定储存模式.
- 当P=N时: 能量E=0, 网络达到容量极限,记忆模式不再稳定。
- 当P>N时: 能量E>0, 交叉项主导能量,网络无法储存模式.
CANN 连续吸引子网络
CANN与hopfield网络的核心原理相似,但应用和表现形式有所不同. 相比于hopfield 网络记住的是一个一个离散的图样(比如图像A,B,C) CANN记住的则是连续的变量(如: 空间方位、眼睛视线方向、头部朝向等). 同时在经典形式下该网络并不具备学习能力.
网络结构
CANN 是由 N 有序个神经元组成的网络,每个神经元代表一个连续变量空间中的取值点. 比如,假设有 8 个神经元,分别编码头部方向 $\theta$:$\theta_1\sim\theta_8$之间按序排列为一个环4, 每个神经元与自己排序上相邻的神经元之间有强连接, 而与距离越远的神经元连接强度越弱甚至是负连接(抑制). 同时网络结构应该具有平移不变性,即: 任何位置都有同样结构的连接.
相关参数: $J_0$: 基线值 (一般是负值,表抑制) $J_1$: 兴奋强度 $\sigma$: 控制兴奋区域的宽度 $\mid{x_i-x_j}\mid$: 变量空间中两个神经元位置之差
连接权重: $$ w_{ij}=J_0+J_1\cdot e^{-\frac{(x_i-x_j)^2}{2\sigma^2}}\qquad exp\left(-\frac{(x_i-x_j)^2}{2\sigma^2}\right) $$ 网络动力学: $$ \tau\frac{du_{i}(t)}{dt}=-u_i(t)+\sum_jw_{ij}f(u_j(t))+I_i(t) $$ 其中f(u)是非线性激活函数(如: ReLU或sigmoid); $I_i(t)$是外部输入,$\tau$是时间常数(电位变化快慢的惯性).
核心原理
CANN的主要功能是模拟仿真,而不像hopfield一样可以用来进行分类(聚类). 依旧以方向为例, 假设有180个神经元编码360°的方向,
- 假设目标显示受到了50°的刺激. 此时50°对应的神经元和附近的5神经元会接收到一个电流输入(以高斯分布为例): $$ I_i=I_0\cdot exp\left(-\frac{(x_i-x_j)^2}{2\sigma^2}\right) $$ 随后网络中的神经元会按照上述的动力学公式传递信号, 最终网络趋于稳态, 并在50°位置维持一个峰.
- 此时若平滑改变方向从50°到60°, 那么网络会动态调整峰的分布, 在可视化窗口可以看到小峰缓慢向60度移动的过程.
除此之外, 由于该网络的对称性和平移不变性, 输入信号后,较远的神经元都被抑制或者无法兴奋,因此最终信号会汇聚在对应位置形成较强的尖峰.
